콘텐츠

• 지침
• 어떻게
• 필요한 것

사다리꼴의 부피를 계산하는 수학적 과정을 이해하는 것은 개념적이고 실제적인 과학적 구조의 기하학의 핵심을 통과합니다. 아래 텍스트는 필수 공식 방정식의 변수에 수반되는 기본 원리를 먼저 이해하고이를 사다리꼴 수치와 관련된 문제를 해결하는 데 사용하기위한 단계별 절차입니다.

지침

사다리꼴의 부피를 계산하는 수학적 과정을 이해하는 것은 개념적이고 실제적인 과학적 구조의 기하학의 핵심을 통과합니다. Fotolia.com에서 jaddingt하여 수학 이미지 ()

1. 주거용 또는 상업용 건물, 진흙 침대 및 집 파이프 및 기타 시설과 같은 토양 작업과 같은 실용적인 프로젝트의 건설이 닫힌 평평한 인물 내에서 액체 물질의 양에 대한 필요한 지식을 필요로 함을 이해하면 학생이 볼륨을 계산할 필요성에 대한 이해. 기존 치수를 정확하게 측정하면 정확한 부피 계산이 가능합니다.

   실제적으로, 지형 분지의 점토 벽의 횡단면으로서 사다리꼴을 발견하는 것은 사다리꼴을 정의하는데 유용합니다. 4면 그림의 두면이 평행하지만 크기가 같지 않고 다른 두면이 평행하지 않으면이 그림을 사다리꼴이라고합니다.

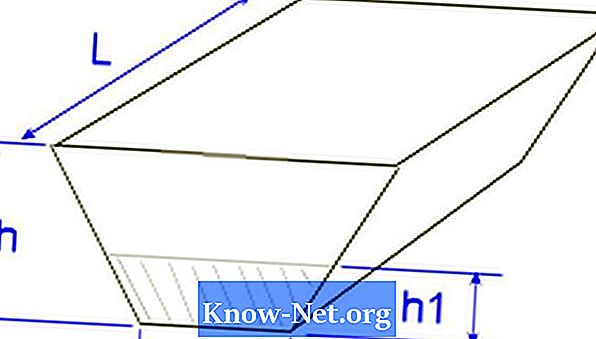
   따라서 22.86m 길이의 그림이있는 경우 전면 크기는 너비가 17.37m, 높이가 10.66m이며 너비가 21.94m이고 너비가 3.65m입니다 높이, 볼륨을 계산하려면 다음과 같이 진행합니다 :

   1. 모양은 정면에서 17.37 x 22.86의 직사각형으로 생각할 수 있습니다. 바닥에서 22.94 x 3.65의 평면에 22.86 m의 거리에 부착됩니다.

   2. 이 방법으로 볼륨을 계산하는 수식은 앞뒤 대신 직사각형의 꼭대기와 밑면이있는 트렁크로 그릴 수 있으며, V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3이고, 여기서 변수는 a1 = 17,37; b1 = 10.66; α21D = 21.94; b2 = 3.65; h = 22.86 : V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3V = [17.3710,66 + 21,943,65 + (17,373,65 + 21,9410.66) / 2] * 22.86 / 3V = [265.60 + (63.54 + 234.11) / 2] * 7.62V = [265.60 + (297.66) / 2 ] 7.62V = [414.44] 7.62V = 3158.03m³

      
      

2. 형식에 따라, 사다리꼴의 동적 볼륨은 정적 인 사다리꼴이 기하학적으로 2 차원 그림이기 때문에 정적 모델의 동적 볼륨과 다릅니다. 계산할 영역은 종이에 2 차원으로 그려진 사다리꼴 일 수 있습니다. 따라서 평균 너비와 길이를 사용하는 수식의 다른 버전은 다음과 같습니다. V = [a1b1 + a2b2 + 4 ((a1 + a2) / 2 * (b1 + b2) / 2)] * h / 6 사각형의 꼭대기와 아래쪽 사각형의 평균 변을 말합니다.

3. 2 단계의 동적 적용에서와 같이 수영장이나 밀폐형 실린더와 같은 사다리꼴 구조의 부피는 특정 높이의 미터당 리터로 계산할 수 있습니다. 이것은 전체 컨테이너의 체적을 높이로 나눈 값이 적절한 비율을 얻음을 의미합니다. 입방 미터를 얻기 위해 공식 (m 단위)을 사용하십시오.

   원통형이 아닌 용기의 경우 비율은 학생이 원하는 경우 깊이에 따라 다릅니다. 그리고 이것은 용기가 부분적으로 가득 차 있고 부피가 다른 수준에서 결정될 것임을 의미한다고 생각할 수도 있습니다. 즉, 부피는 높이의 함수입니다.

4. a 방향의 폭이 a1에서 a2로 직선적으로 변화함에 따라 a = a1 + (a2-a1) k = (1-k) a1 + ka2; kh는 바닥에서부터 상승한다 (k는 0에서 1까지이다). 동일한 방식으로, b = b1 + (b2-b1) k = (1-k) b1 + kb2; 높이 kh, 밑변 a1을 b1, 꼭지점 a를 b로 한 솔리드의 부피는 V (k) = [a1b1 + ab + a1b / 2 + ab1 / 2] * kh / 3이다.

   비율 k 대신 실제 값을 사용하면 k = L / h를 대입하면 V (L) = [(3h ^ 2-3Lh + L ^ 2) a1b1 + L2a2a2b2 + (3Lh-2L2) (a1b2 + a2b1) / 2] * L / (3h ^ 2)이다. 이것은 우리에게 깊이의 함수로서의 볼륨을줍니다.

   
   

5. 사다리꼴의 체적을 계산하는 것은 사다리꼴 그림이 2 차원인지 3 차원인지를 해석하는 능력을 포함합니다. 사다리꼴 해석 공학 측면의 역동적 인 실습은 사다리꼴 그림이 단순히 종이에 볼륨 또는 단순한 스케치가 포함되어 있는지 여부에 관계없이 단순히 그려지거나 구성되는 것인지 여부를 중심으로 진행됩니다.

어떻게

• 기하학적 문제를 해결하면 수식이 어떻게 그리고 왜 왜 그런지, 그리고 왜 높이가 중요한 변수인지 이해할 수 있습니다. 예를 들어 Hewlett-Packard 공학용 계산기를 사용하여 수동으로 얻은 답을 확인하는 것이 완전한 정확성을 얻는 좋은 방법입니다.

필요한 것

• 연필
• 노트북 시트 (줄이 있거나 없음)
• 눈금자